ノートの使い方（数学）

目次

• ○  数学は「書く」科目です。
• ○  ① 数量（計算）・方程式／確率
• ○  ② 関数（比例・反比例／一次関数／二次関数）
• ○  ③ 図形（平面図形・空間図形／作図）
• ○  ④ データの分析（代表値、箱ひげ図）
• ○  まとめ

数学は「書く」科目です。

受験期に入ってブログ更新がなかなかできませんでした。英語のお話をしたので、今回は数学の話をしましょう。

　普段の指導でもよくお話しすることなのですが、「書くこと」を煩わしい、面倒だと思わないようになることがとても大切です。

　数学はいくつかの分野に分けてお話しすることができます。（話を単純化するために中学内容の数学に限定しましょう。）

① 数量（計算）・方程式／確率
② 関数（比例・反比例／一次関数／二次関数）
③ 図形（平面図形・空間図形／作図）
④ データの分析（代表値、箱ひげ図）

大まかに分ければ以上の4つです。そのいずれの分類においてもノートに何らかの物事を「書く」ということが重要です。

では分類ごとに何を「書く」べきかをお話ししましょう。

① 数量（計算）・方程式／確率

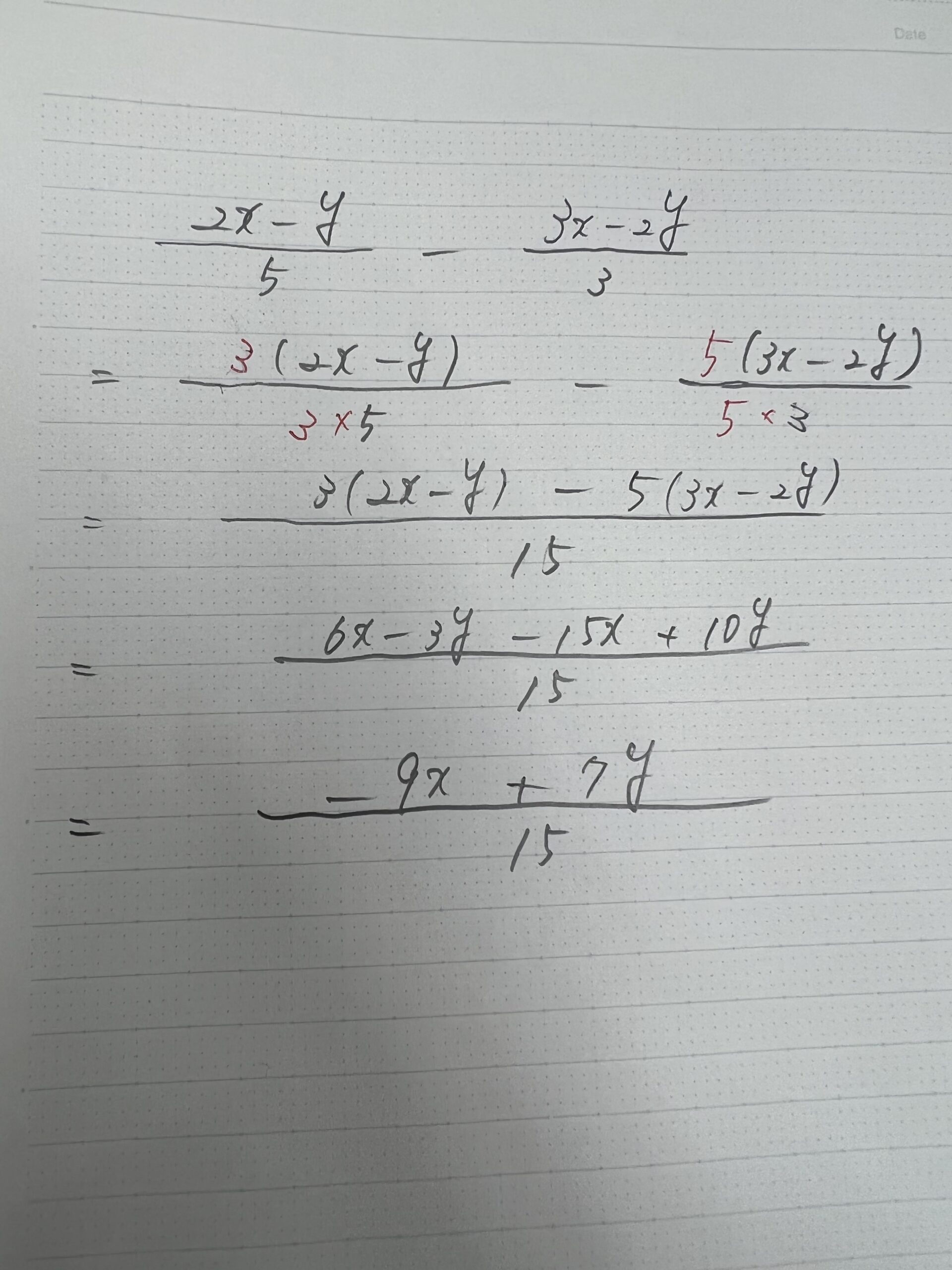
計算問題・方程式を解くといった内容においては
・まず、問題文を正しく写すこと
・次に計算過程を少しずつ変化させた途中式を書くこと
ができていますか？　ここで大切なのは愚直なほど途中式を丁寧にまず書くことです。いかに速く解けても正解できなければ意味がありません。まずはこれでもかというくらいに丁寧に途中式を書いて、多少時間がかかっても全問正解を目指しましょう。その上で、自分にとって省略しても問題のない内容は書かずに済ませられるようになるでしょう。また、分数を含む文字式の計算などは、手順なども身に着ける必要があります。画像の計算を見てください。通分することで分子だけの計算に集中できるようになります。
　　方程式の割合や速さの文章題では、問題内容を整理した図を書くことも必要です。問題の形式に合わせた図が存在しますから、そういった図を書く練習が必要です。

② 関数（比例・反比例／一次関数／二次関数）

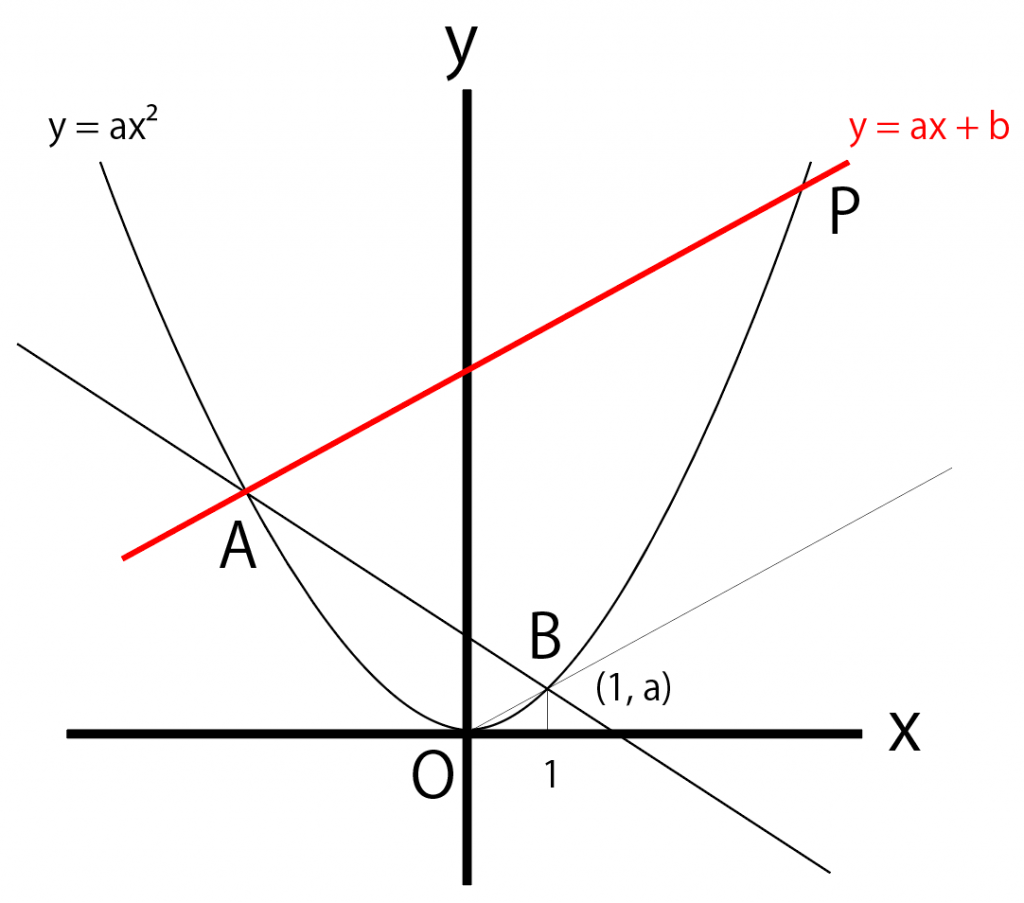
関数は、式とグラフの対応を理解することが重要です。式の意味がグラフ上で表現できているか、またグラフから式に必要な数値を読み取ることができるか、確認してください。また、関数の応用問題では、図形と絡んだ問題が多く出題されます。面積が関係する問題（等積変形）では図を書くことで解法が見えてくる問題もあります。

③ 図形（平面図形・空間図形／作図）

図形こそ、図を書かなければならない単元です。空間図形では見取り図だけではなく、断面図や立面図、投影図といった図を書くことが必要になります。ここで大切なのは求めるべき長さが正確に表せる図を書くことです。見取り図ではどうしても奥行きがあるために正しい長さを表現することができません。正面から見た図であれば長さを正確に表すことが可能です。
　また、平面図形においても完全に正確である必要はありませんが、違和感のない図を書くことができるかどうかはとても大事な要素です。違和感のない図とは、例えば長さの大小関係や、●倍といった数量関係に整合性がある図や、角度がある程度正確な図です。

④ データの分析（代表値、箱ひげ図）

この分野では度数分布表や箱ひげ図といった決まった書くべきものがあります。問題の趣旨に合わせて適切な図を書くことが必要です。

まとめ

ノートが単なる解答用紙になっていませんか？　ノートは本来、問題を解くうえで
情報を整理し、図や表に表す場であり、考え方を式として示す場です。そこにあなたの考えや解くための方針などいろいろな過程が残されていいはずです。きれいなノートは知識をまとめたり、覚えたりする面ではよいノートかもしれません。しかし、考え、解くような内容では理想的なノートとは言えないと思います。

　今一度自分のノートの使い方を見直してみてください。

　慶伸塾では、問題の解法はもちろん、途中式を書く習慣がない生徒さんに対して、途中式を書くように指導しています。また、問題に対応した図の書き方や、その図の意味についても可能な限りお伝えしています。学習相談でお越しの場合は可能であればノートや学校のワークをお持ちください。普段の姿を拝見することでより詳細なお話ができると思います。ご相談希望の方はTEL：0297-84-1570までご連絡をお待ちしております。なお、毎年のことですが、3/4～10の期間はお休みを頂戴しておりますので予めご了承ください。

　今回も最後までお読みいただきありがとうございました。